Игровые автоматы с высокой волатильностью: Математика риска и дисперсии

By Елена Петрова

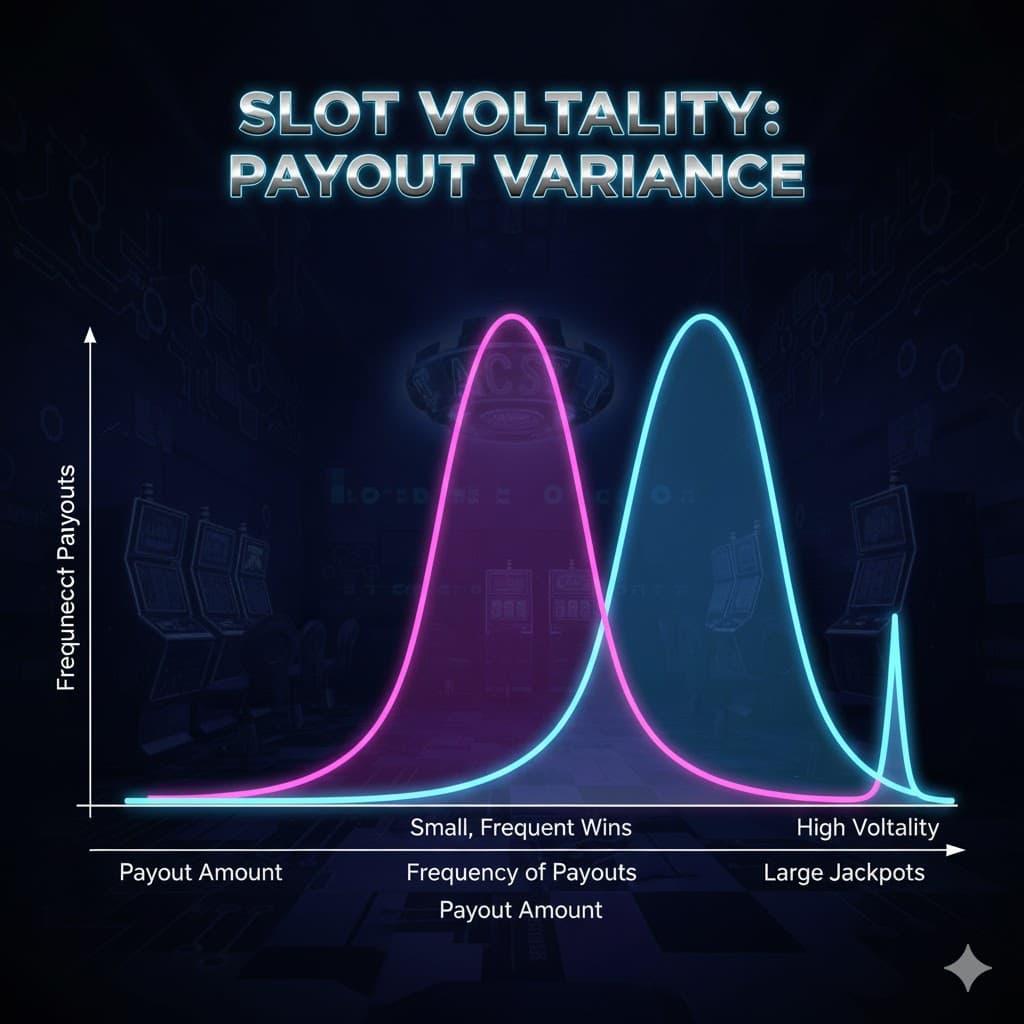
Казино продают мечту о “большом выигрыше”. Разработчики рекламируют это как “Высокая волатильность”. Но как математик, я смотрю на листы PAR. Я смотрю на дисперсию. Цифры рассказывают другую историю, чем рекламные баннеры.

Волатильность не просто модное слово. Это статистическая мера риска. Она определяет вероятность выживания вашего банкролла. Она определяет, будете ли вы играть десять минут или десять часов. Большинство игроков игнорируют это. Они смотрят на возврат игроку (RTP) и считают, что выплата 96% означает безопасность. Это математическая ошибка.

В этом анализе я разберу механику высоковолатильных слотов. Мы рассмотрим стандартное отклонение, соотношение между частотой выигрышей и размером выплат и почему “высокий риск” не всегда равен “высокой награде”. Здесь мы оперируем фактами, а не ложными надеждами.

Определение волатильности: это просто дисперсия

В теории вероятностей волатильность синонимична с дисперсией или стандартным отклонением. В контексте игрового автомата она измеряет, насколько результаты отклоняются от ожиданий в среднем.

Представьте себе игру с RTP 100% (теоретическая невозможность в онлайн-казино, но полезная для этого примера). Вы ставите 1,00$.

• Низкая волатильность: Вы ставите 1,00$. Вы выигрываете 0,90$ или 1,10$ почти на каждом спине. Отклонение от среднего значения невелико. Ваша линия на графике ровная.
• Высокая волатильность: Вы ставите 1,00$. Вы теряете 1,00$ в течение 99 спинов. На 100-м спине вы выигрываете 100$. Среднее то же самое. Опыт жесткий.

Высоковолатильные слоты запрограммированы с огромным стандартным отклонением. “Пустые спины” — это цена, которую вы платите за необычные выигрыши. Математика требует длинной серии проигрышей, чтобы компенсировать огромный потенциал выплаты в 10,000x или 50,000x вашей ставки.

Индекс Волатильности (VI) объясняется

Студии игр не просто догадываются о волатильности. Они рассчитывают Индекс Волатильности (VI). Это часто является значением, основанным на доверительном интервале симуляции.

Когда я анализирую игру как Book of Dead or Money Train , я смотрю на распределение выигрышей. В играх с высоким VI значительная часть общего RTP скрыта за “редкими событиями”. Эти события, как правило, являются бонусными раундами или специфическими комбинациями символов.

Например, в стандартной игре с низкой дисперсией 40% от RTP может поступать из выигрышей базовой игры от 1x до 5x. В игре с высокой дисперсией выигрыши в базовой игре могут составлять только 15% от RTP. Остальная возвратимость скрыта в вероятностном событии 1 из 200 спинов. Вы оплачиваете спины, которые математически не могут принести ценности, до тех пор, пока не сработает это конкретное событие.

Связь между частотой выигрышей и волатильностью

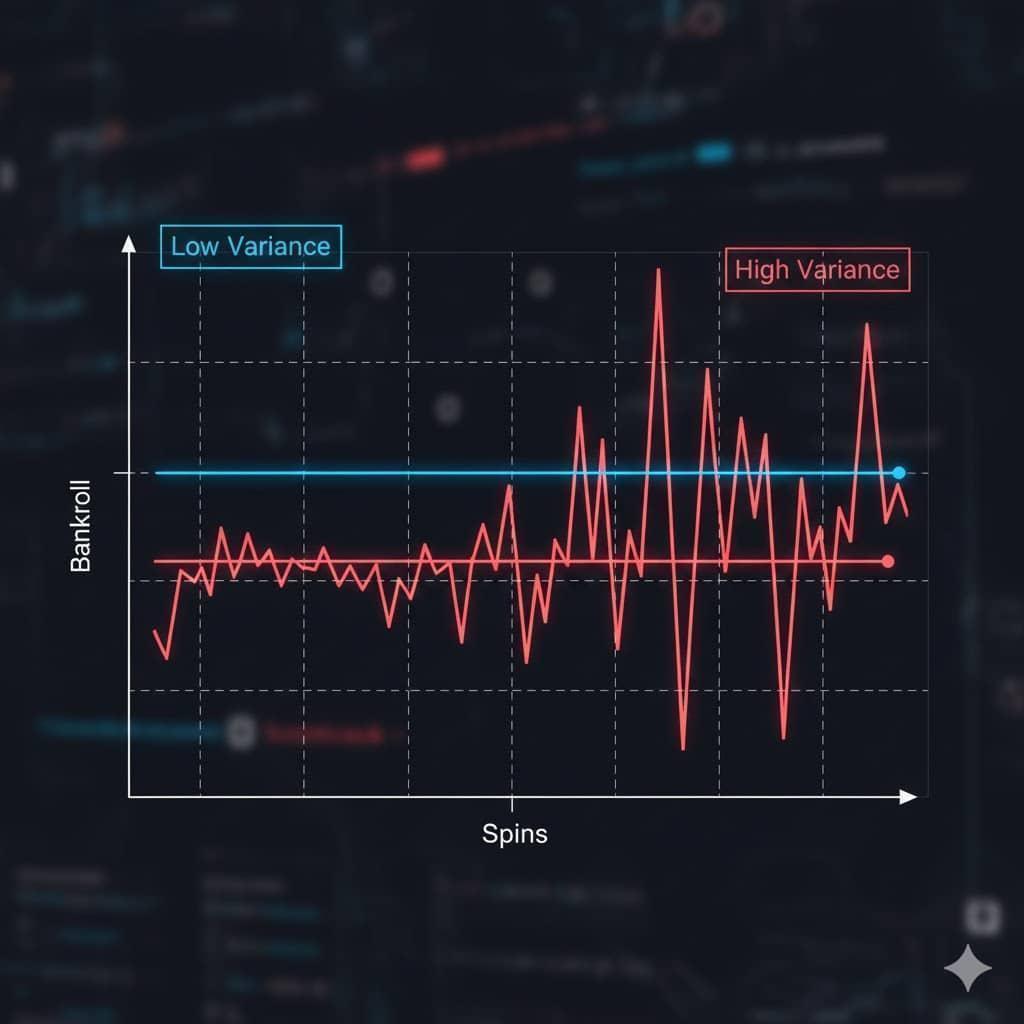
Существует сильная отрицательная корреляция между волатильностью и частотой выигрышей (HF). Частота выигрышей — это процент вращений, которые приводят к any выплатам (даже если они меньше суммы ставки).

Низкая волатильность: HF часто составляет 30% – 40%. Вы постоянно получаете положительное подкрепление. Автомат развлекает вас маленькими звонками и свистками.

Высокая волатильность: HF может упасть до 10% – 20%. Это означает, что 80% – 90% ваших вращений мертвы. Это «сухая полоса». Математически это приводит к гибели большинства банкроллов.

Феномен «ложной победы»

Высоковолатильные слоты часто используют «ложные победы», чтобы скрыть низкую частоту выигрышей. Вы ставите 2,00$. Экран мигает, звучат звуки, летят монеты. Вы выиграли 0,50$.

Ваш мозг регистрирует это как выигрыш. Ваш банкролл — это потеря в 1,50$. Высоковолатильная математика полагается на эти ложные победы, чтобы технически поддерживать более высокую частоту выигрышей, не отдавая фактически RTP, зарезервированный для верхних призов.

Механика банкролла: вероятность потери

Почему я постоянно предупреждаю о размере ставок в играх с высокой волатильностью? Потому что существует формула «риск потери».

Поскольку дисперсия высока, снижение круче. Если вы взяли 50 ставок на игру с низкой волатильностью, у вас высока вероятность играть в течение часа. Если вы взяли 50 ставок на игру с высокой волатильностью, вероятность достижения нуля, прежде чем сработает бонус, статистически вероятна.

Математика выживания: Чтобы выжить при стандартном отклонении высоковолатильного слота, вам нужен банкролл минимум в 200x – 300x вашего среднего размера ставки. Все, что меньше, — это ставка на удачу, а не игра по вероятностям.

Почему RTP сбивает с толку в играх с высокой дисперсией

RTP — это долгосрочный теоретический расчет. “Долгосрочный” в симуляции автоматов означает миллиарды спинов.

Если у слота с высокой волатильностью RTP составляет 96,5%, это число не имеет значения для вашей сессии из 500 спинов. Из-за высокой дисперсии ваш личный RTP за эту сессию может быть 40% или 400%. RTP стабилизируется только на бесконечном горизонте. Не доверяйте метке RTP на высокодисперсном автомате, чтобы спасти вас в краткосрочной перспективе. Этого не произойдет.

Топовые слоты с высокой волатильностью: математический взгляд

Мы видим, как на рынок выходят многие «экстремальные» слоты. Вот как обстоят дела с самыми популярными.

Серия Money Train (Relax Gaming)

Это эталон для высокой дисперсии. RTP приличен (около 96,4%), но распределение сильно смещено в сторону бонуса Money Cart. Базовая игра, по сути, является залом ожидания. Дисперсия здесь экстремальна; вы покупаете билеты на лотерею, которая разыгрывается каждые несколько сотен спинов.

Dead or Alive 2 (NetEnt)

Классика. Максимальный выигрыш в 111 111x — это отклонение, которое управляет математикой. Чтобы профинансировать максимальный выигрыш такой величины, миллионы спинов должны закончиться нулевыми результатами. Это эффективная математика, но жестокая для случайного игрока.

San Quentin xWays (Nolimit City)

Nolimit City доводит индекс волатильности до предела. С потенциальной выплатой 150000x, стандартное отклонение зашкаливает. Опции “покупки функции” существуют, потому что органическая частота выигрышей главных функций статистически ничтожна.

Заключение: Понимание кривой

Я не испытываю неприязни к слотам с высокой волатильностью. Я играю в них. Но я играю, понимая распределение кривой. Я знаю, что пустые вращения — это математическая необходимость, а не ошибка.

Если вы решили играть в эти игры, примите дисперсию. Уменьшите размер своей ставки. Игнорируйте “почти упущенные”. Математика предназначена для проверки вашего терпения. Если вы не можете справиться с колебаниями, придерживайтесь столов с низкой дисперсией. Цифры не заботятся о ваших чувствах.

Часто задаваемые вопросы